扫二维码与项目经理沟通
我们在微信上24小时期待你的声音
解答本文疑问/技术咨询/运营咨询/技术建议/互联网交流
本小白学习了Pytorch优化器以及其中内置的一些深度学习优化算法之后,写下这篇总结博客,水平有限,希望路过的各位客官不吝赐教,多多指正。
本文的目录如下:
机器学习模型的训练步骤

众所周知,机器学习模型的训练过程包含了上图所示的几个重要部分。
Pytorch中优化器的功能为:管理和更新模型中可学习参数的值,使得模型输出更接近真实标签。
在Pytorch中,自动求导模块可以根据损失函数对模型的参数进行求梯度运算。优化器会获取得到的梯度,然后利用一些策略去更新模型的参数,最终使得损失函数的值下降。
torch.optim
2.Optimizer类的基本属性

上图为Pytorch源码中Optimizer类的初始化函数,从中可以看出,有基本属性有三个:
首先,defaults这个属性,这是存储的优化器中的超参数,比如学习率,momentum的值等等。然后state这个属性存储的是一些参数的缓存,比如使用动量momentum的时候,他会使用到前几次的梯度值,前几次梯度的值就是存储在state这个属性当中。最后,第三个属性就是pytorch优化器最重要的属性——param_groups,它是用来管理参数组的,其作用是存储我们模型中使用的一系列参数的。在Optimizer类的初始化函数中可以看出,param_groups的类型是一个list,其中的每一个元素是一个字典,每个字典的key值才是存储的参数值。
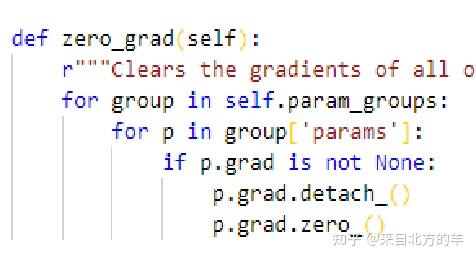
在pytorch中每个参数都是一个张量,每个张量会有一个记录其梯度的属性值grad。zero_grad()函数的作用为清空每一个参数梯度值。在pytorch中,每一次进行反向传播的时候,自动求导器得到的梯度,会加到张量已有的grad属性上面。pytorch中的这个设定跟我们内心所想并不一致。因此,我们在使用完梯度,或者是在进行梯度求导之前,需要把已有的梯度进行清零。这就是zero_grad的需要使用的原因。
在zero_grad()函数的源码中,首先它会对param_groups进行一个for循环,我们知道param_groups是一个list,我们取出来的每一个元素是一个字典。这个字典有很多的key,最终要的就是params这个key对应的value。这样我们就可以取出参数,这个参数又是一个list,再对参数的list进行for循环,这样就取出了每一个具体的参数。每个参数的类型是张量,张量包含着梯度属性。之后判断grad属性是否非空,如果grad不为零,我们就把参数从计算图上进行detach(不能参与梯度运算),然后清零。这样就实现了一个梯度清零的操作。由于pytorch是动态图,detach掉的动态图在前向传播的时候会重新构图。
当我们反向传播获得了梯度之后,就需要通过step()方法进行一步的权值参数更新
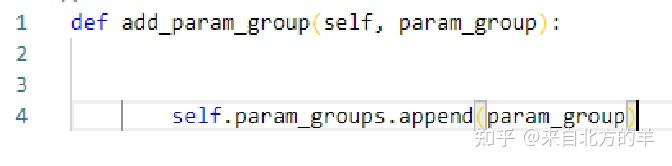
优化器需要管理很多的参数,pytorch中可以对不同的参数进行分组。参数分组后可以对每组的参数设置不同的超参数,比如对模型的不同参数设置不同的学习率。param_groups是一个list,每个元素中存储的是一组参数。这个函数接收的参数是param_group,是一个字典。

可以看到该函数返回的是个字典,字典有两个key。一个是state键对应的value,刚才说过这里边存储的是缓存信息。还有一个是param_groups键对应的value里边存储的是管理哪些参数。
该函数和刚才state_dict()函数的功能刚好相反,功能是加载装填信息字典,该函数接受到的是一个状态字典,然后放到优化器当中。
state_dict(),state_dict()两个函数可以实现模型的断点续训练。如果模型训练到一半有事要停下来,完事下次还想从上次训练的地方接着训练,就可以使用这两个函数来完成这个事情。
4.1常见的深度学习优化算法
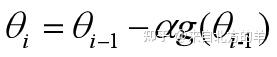
函数某一点处的梯度的方向是此处变化率最大的方向。梯度下降法则在每次的迭代中选择梯度 和学习率
的乘积作为修正量。下图为梯度下降法每次迭代过程的示意图。
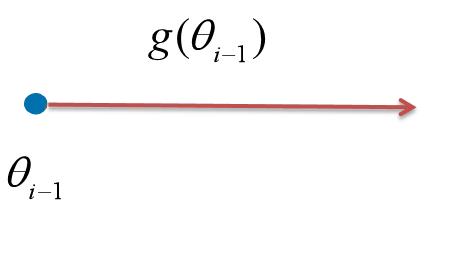
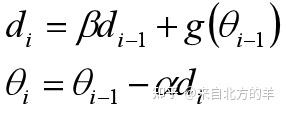
在动量法的每次迭代当中,增加了上一轮迭代过程的修正量 。相当于在每次迭代过程中引入了之前迭代的“惯性”。关于该方法网上也有很多类似的帖子来进行讲解。该算法和以下的形式等价:
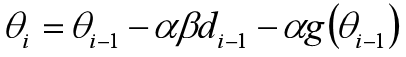
可以理解为,每次迭代的修正量为梯度 和惯性
的和。下图为Momentum动量法每次迭代过程的示意图。
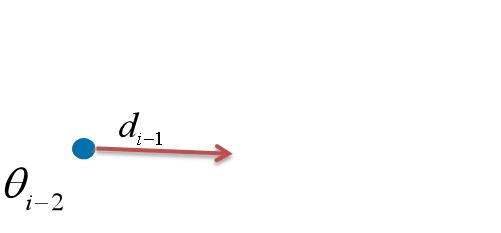
Momentum dampening为pytorch优化器自带的内容,没有找到相关的解释。看了一下源码,得到了以下的形式:
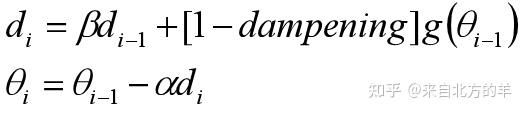
其中dampening的取值范围为0~1。虽然名字叫做Momentum dampening,但是该方法是对梯度值进行的衰减。
另外,如果有正则化的情况下,Momentum dampening是对梯度和正则化项的和进行衰减,具体形式如下:

NAG的原始形式为:
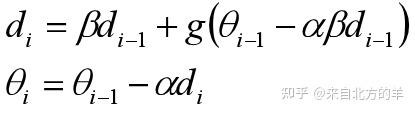
其等价形式为:
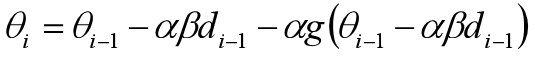
对于该方法,参考很多网上的博客给出的解释是,提前往前(沿着动量的方向)走一小步,能够让算法提前看到前方的地形梯度。如果前面的梯度比当前位置的梯度大,那我就可以把步子迈得比原来大一些,如果前面的梯度比现在的梯度小,那我就可以把步子迈得小一些。这个大一些、小一些,都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。关于动量法和NAG方法的详细介绍,强烈推荐:
郑华滨:比Momentum更快:揭开Nesterov Accelerated Gradient的真面目上述帖子中,对NAG的参数更新公式进行了进一步的推导:
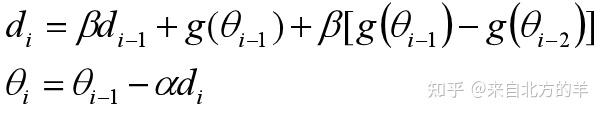
从这个形式可以看出来,NAG相当于在普通的动量方法中加入了二阶导数信息。上过优化方法课的同学会知道,利用二阶梯度的优化方法会比利用一阶梯度的方法收敛要快。下图为NAG法每次迭代过程的示意图。

上述的优化方法以固定的学习率更新每个参数,但深度神经网络往往包含大量的参数,这些参数并不是总会用得到。对于经常更新的参数,我们已经积累了大量关于它的知识,不希望其被单个样本影响太大,希望其学习速率慢一些。对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。为了解决梯度下降算法中学习率固定的问题,有学者提出了Adgrad。该算法引入了一个东西叫做二阶动量,这个二阶动量就是参数的历史梯度的平方总和。Adagrad学习率将与历史梯度和成反比,也就是说较大梯度具有较小的学习率,而较小的梯度具有较大的学习率,可以解决普通的梯度下降方法中学习率一直不变的问题。但是该方法的缺陷在于,需要自己手动指定初始学习率,而且由于分母中历史梯度一直累加,学习率将逐渐下降至0,并且如果初始梯度很大的话,会导致整个训练过程的学习率一直很小,从而导致学习时间变长。
该算法的原始形式如下:
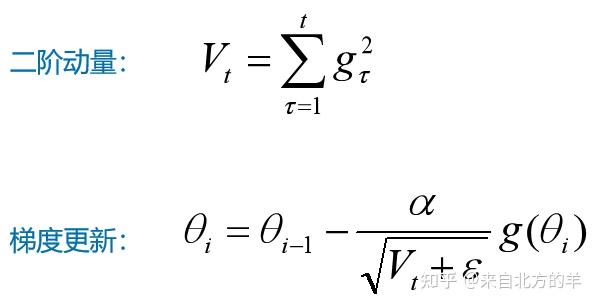
有学者认为AdaGrad单调递减的学习率变化过于激进,并且其考虑的是参数的所有历史梯度,对于那种历史比较久远的梯度,可能不具备参考价值了。因此有学者提出了一个想法:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。RMSprop就是利用了这个思想。其中把平方和形式的二阶动量转变成了,一个叫做历史梯度的指数加权平均值的东西。
指数加权平均(参考贴)
指数加权平均(exponentially weighted averges),也叫指数加权移动平均,是一种常用的序列数据处理方式。
它的计算公式如下:
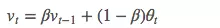
其中,
举个温度预测的例子来说明指数加权平均的作用:
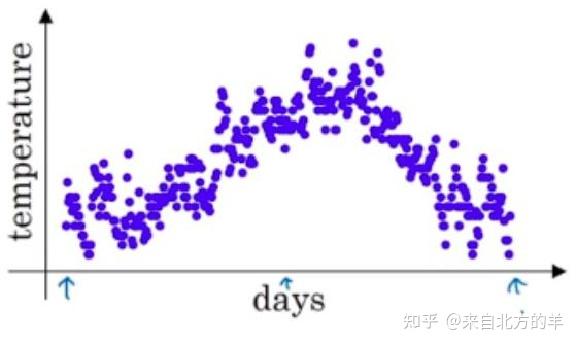
假如测量连续一百天的温度变化,实际的测量值是包含非常大的噪声的,因此数据的波动非常的大。利用指数加权平均值对每天的温度进行平滑,其中第100天的温度平滑后的值如下所示:
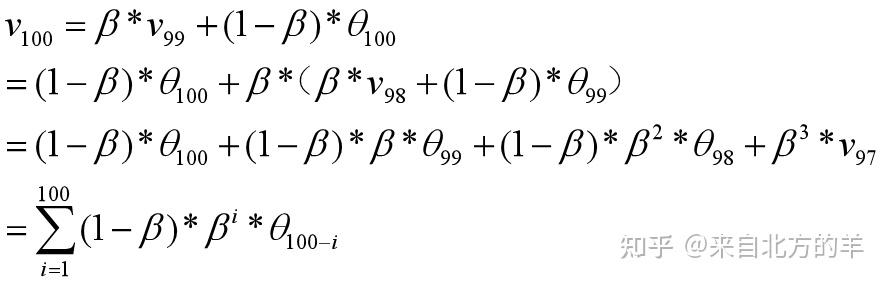
可见,不同温度值的加权因子随着距离当前的时刻的距离呈现指数衰减。因此指数加权平均值可以有效的利用附近数据的信息。前文所述的Momentum动量法,其实也可以理解为对历史梯度进行指数加权平均。
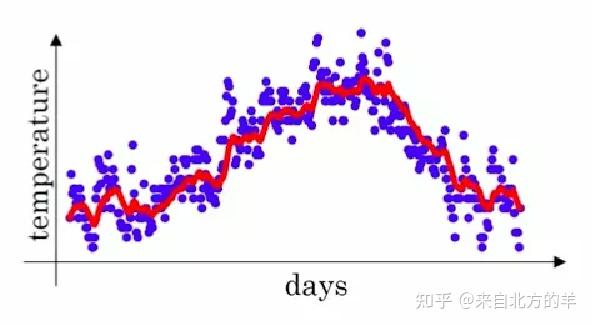
RMSProp的形式如下:
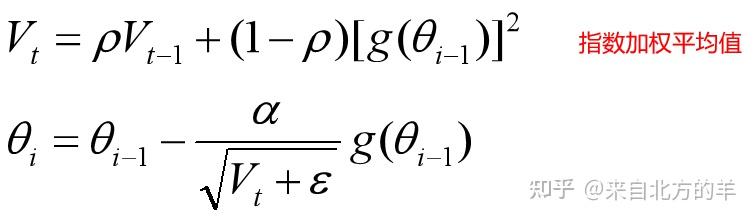
RMSProp算法将AdaGrad算法中的的二阶动量转换成了历史梯度的加权平均值的形式。减少了计算量的同事,也有利于利用较近时刻的梯度信息。
AdaDelta相比之前的RMSprops,借鉴了牛顿法的思想。牛顿法的具体内容可以参考如下帖子:
Eureka:梯度下降法、牛顿法和拟牛顿法牛顿法的一阶的原始形式如下:
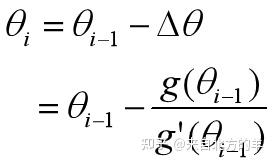
其中二阶梯度的倒数可以做如下的近似(具体的原理参考该贴):
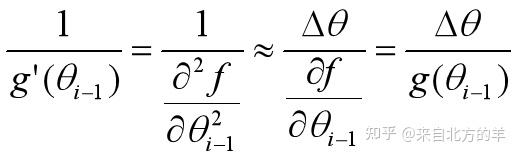
则牛顿法的原始形式可以近似为如下形式:
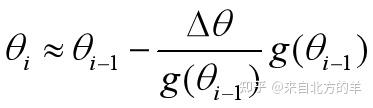
先呈上AdaDelta算法的具体形式:
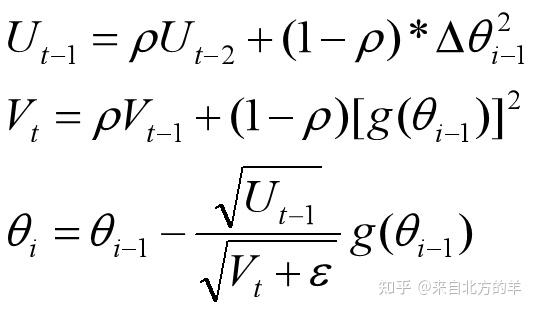
其中, 和
计算的是
和
的指数加权平均值。其中第三行才用的是牛顿法的迭代形式。分子的下标是t-1,分母的下标是t。这是因为当
计算出来的时候
还没有计算出来。
Adam的核心思想是在RMSProp增加了动量的。除了增加了动量,Adam算法中还对历史梯度才用了求指数加权平均的方法。简化版本的Adam算法代码如下图所示。

完整版Adam更新算法额外增加了一个偏置(bias)矫正机制。

因为 和
两个矩阵初始值很小,在算法没有“热身”完成之前存在偏差,需要采取一些补偿措施。在算法迭代的初期,
和
的值比较大,可以对较小的
和
的值进行一定程度方法。当迭代进行较久的时候,
和
的值接近0,此时相当于对
和
的没有进行修正。
Adamax
SparseAdam
ASGD
Rprop
LBFGS
其他算法等日后弄明白来填坑。。。。。。
4.2常见的深度学习优化算法在pytorch中的调用
在pytorch中提供了torch.optim来优化我们的神经网络,torch.optim是实现各种优化算法的包。4.1中的所有的方法都已经支持。具体用法参考torch.optim文档。以下介绍每种优化算法的接口如何使用,其中每个参数的具体含义参考前文。

params(iterable)- 参数组,优化器要管理的那部分参数。
lr(float)- 初始学习率。
momentum(float)- 动量因子,前文的 ,通常设置为0.9,0.8
dampening(float)- dampening for momentum ,如前文所述的Momentum dampening,值得注意的是,若采用nesterov,dampening必须为 0.
weight_decay(float)- 权值衰减系数,也就是L2正则项的系数
nesterov(bool)- bool选项,是否使用NAG(Nesterov accelerated gradient)

params(iterable)- 参数组,优化器要管理的那部分参数。
lr(float)- 初始学习率。
lr_decay:设置学习率衰减
weight_decay(float)- 权值衰减系数,也就是L2正则项的系数
eps:浮点相对精确度,接触过matlab的同学应该接触过这个东西。

params(iterable)- 参数组,优化器要管理的那部分参数。
lr(float)- 初始学习率。
momentum(float)- 动量因子,前文的 ,通常设置为0.9,0.8
alpha(float)- 平滑常数,也就是前文所述的指数加权平均值计算公式中的
eps:同前文所述
centered:如果设定为True,会对历史梯度进行方差标准化。
weight_decay(float)- 权值衰减系数,也就是L2正则项的系数

params(iterable)- 参数组,优化器要管理的那部分参数。
rho(float)-平滑常数,也就是前文所述的指数加权平均值计算公式中的
eps:同前文所述
lr(float)- 初始学习率。
weight_decay(float)- 权值衰减系数,也就是L2正则项的系数
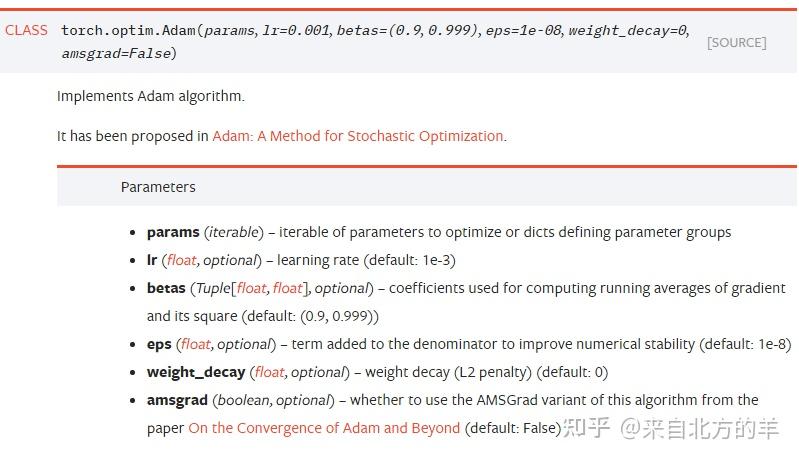
params(iterable)- 参数组,优化器要管理的那部分参数。
lr(float)- 初始学习率。
betas(Tuple)-前文所述的
eps:同前文所述
weight_decay(float)- 权值衰减系数,也就是L2正则项的系数
amsgrad(boolen):是否使用AMSGrad
等日后来填坑

我们在微信上24小时期待你的声音
解答本文疑问/技术咨询/运营咨询/技术建议/互联网交流