扫二维码与项目经理沟通
我们在微信上24小时期待你的声音
解答本文疑问/技术咨询/运营咨询/技术建议/互联网交流
本人方向为slam。因为想要了解基于优化的slam而选了《凸优化与轨迹规划》这门课,老师在课上讲凸优化和最优化是不同的。我想问一下凸优化和最优化有何不同?明明凸优化与最优化中的算法都一样啊(比如都讲到了高斯牛顿法)。以及slam中的优化问题究竟是哪一类优化问题?
最优化两部分:凸与非凸。
其中,凸优化相对来说比较容易可解决:因为凸的性质,只需求解局部最优即为全局最优解。
非凸及非凸优化相对来说范围大、内容难度高,尚未有统一解法。大多数slam问题属于这里。
目前能够解决的非凸问题可以参看这篇
最优化问题中的非线性、非凸规划问题,高效可行的求解算法有哪些?内容的回答。
而slam领域目前按设备来分有激光、视觉、融合三大部分,每部分根据传感器获取的信息维度不同(2d vs 3d vs etc),其各自定义出的优化目标(也不一定有解析表达形式的函数)也千差万别。
主流领域下各自实现的霸榜方向很可能会由业界一两篇paper和规则范式直接逆转风向。目前来说想研究上有突破很吃学历资历,但是实现这块算是开始dl那个味儿了
slam的非凸性主要包含两类:定义域包含rotation 本身非凸集合 而且是非线性约束 实际求解时用到李代数 或者流形上的优化 相当于把问题变成欧式空间上的优化问题 用梯度下降或牛顿法可以求解;outlier的引入 会让目标函数有很多局部极值 导致算法局部收敛 outlier包括前端错误的匹配或回环 总的来说 凸优化对slam很有用 可以增强求解器的鲁棒性和准确度 但那是大佬们的工作 一般人还是搞搞前端容易出成果
Hilbert曾经说过,一个数学问题能正确描述出来,那么就成功了80%。对于一个优化问题而言,如果能转化为凸优化问题,那么就成功了90%。 ——中科大《凸优化》授课老师凌青
最优化(或称数学规划)是一个很大的范畴,它是指找出实数函数 的最大值或最小值。一般最优化问题可写作如下形式[1]:
其中 是
维未知自变量向量,
,而
,
,
是关于自变量的实值函数。集合
是
维空间的一个子集。
被称为目标函数,其它等式、不等式被称为约束条件。
目前最优化问题可以按以下四种方式进行分类:
如我们上面所述需要满足一些等式或者不等式的约束的就是有约束优化,没有则是无约束优化。比如SVM模型的求解就是经典的有约束优化问题,需要用到拉格朗日乘子将其先将其约束转换为目标函数,然后再将其转换为对偶问题进行求解。
根据优化函数的自变量的定义域 是连续的还是离散的,可以将优化问题分为连续优化和离散优化。其中离散优化主要包括整数规划和关于图、拟阵等的组合优化。
线性规划是指目标函数和约束函数都为线性的优化问题(定义域需要连续)。若 是线性函数,则对任意的
和
有下述等式成立:
而非线性规划是指目标函数和约束至少有一个为非线性的优化问题。线性规划一般在运筹学(如 经济模型等)中有重要运用,而非线性规划在机器学习中有着重要的运用。
过去人们认为只有线性规划可以高效求解,而现在有一个普遍的观点认为,优化问题的分水岭不是线性和非线性,而是凸与非凸[2]。凸优化问题是指目标函数和约束函数都是凸函数的问题。若 是凸函数,则对任意的
和
且
有下述不等式成立:
可以看出凸性是较线性更为一般的性质:线性函数需要严格满足等式,而凸函数仅仅需要在 和
取特定值的情况下满足不等式。因此线性规划问题也是凸优化问题,可以将凸优化看成是线性规划的扩展。只要问题可以被转换为凸优化问题,那么就能用内点法等等在多项式时间内求解。凸函数给优化带来很大方便的原因在于其任何一个局部极小点都是全局最优解,便于设计出高效的优化算法。
接下来我们考虑求解算法。我们这里只考虑无约束连续(数值)优化,而不考虑有约束优化与离散优化。
对大多数无约束数值优化算法而言,凸函数和非凸函数都可以拿来用,如梯度下降法[3]、牛顿法[4]、坐标下降法[5]等(当然,对于用到导数的方法,函数得可以求导)。不过,光滑性和凸性会影响到算法的收敛性质,通常来讲更好的凸性和光滑性质会加速算法的收敛。如梯度下降法在光滑强凸函数下可以达到 的线性收敛速率,在光滑凸函数下则达到
的次线性收敛速率,在光滑非凸情况下则只能达到
的次线性收敛速率。
这里需要专门提一下,对于非凸问题而言(如对神经网络的优化),找到其全局最优解是NP-hard的,我们大多数情况下找到的都是其局部最优解。像我们将前面梯度下降法用于非凸问题,其找到的一阶导数为0的点不一定是全局最优点,可能是鞍点。
像几十年前提出的模拟退火、贝叶斯优化这些可以有效解决低维度非凸优化的问题。然而深度学习中大规模神经网络的参数数目巨大,优化问题的维度很高,传统的算法便不再适用。
在此情况下,学者们进行了如下的有益尝试:
至于SLAM中的优化问题究竟是哪一类优化问题,我对SLAM领域不熟就不敢妄议了嘿嘿。
凸优化(凸优化)和最优化(优化)是数学和计算机科学中相关但不同的概念。
最优化(optimization)是指在一定的约束或要求下,找到给定问题的最佳解决方案的一般问题。 这可能涉及找到函数的最小值或最大值、问题的最有效解决方案或满足一组标准的解决方案。 可以使用多种方法解决优化问题,包括数学算法和启发式方法。
凸优化(凸优化)是一种特定类型的优化,涉及寻找凸函数的最小值或最大值。 凸函数是一种数学函数,它具有函数图形上任意两点之间的线段位于图形上方或图形上的特性。 凸优化问题具有某些理想的性质,例如能够被有效地求解和保证全局最优解。
总之,优化是寻找给定问题最佳解决方案的一般问题,而凸优化是一种特定类型的优化,涉及寻找凸函数的最小值或最大值。 凸优化是优化的一个子集,并且共享许多相同的原理和技术。
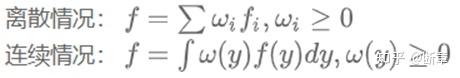
凸(凹)函数的非负加权求和仍是凸(凹)函数;
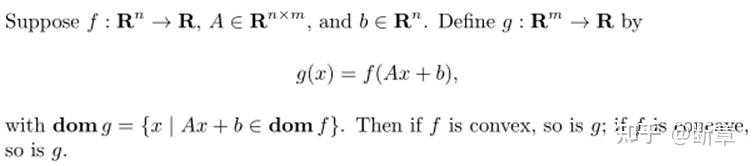

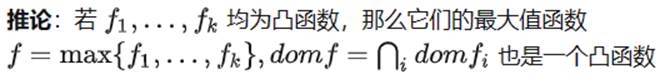

注意这个是部分凸
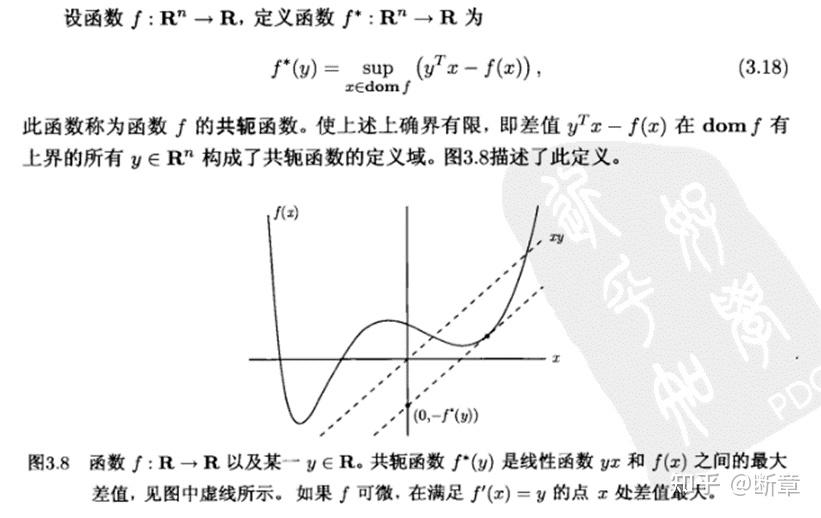
建立凸函数的一个方法:将其表示为一族仿射函数的逐点上确界
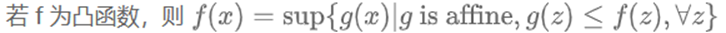
所描述的事情实际上就是f被很多个支撑超平面(以及更靠下的平面)紧紧的围起来了

n=1
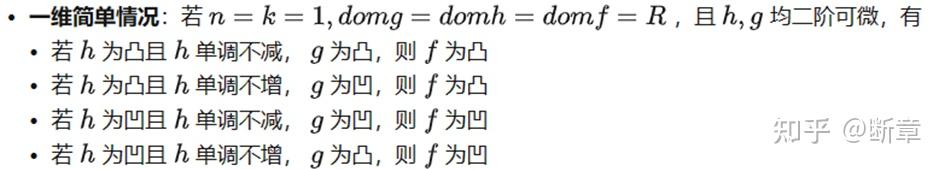
n>1

注意高维情况下是 的单调性一定要满足。






是凸的,所以
也是凸的,一个凸的投影,得到的还是凸的


是凸的(联合凸的),算
,可以先
,再算
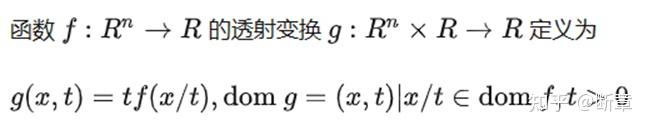
f是凸(凹)的,则g是凸(凹)的。
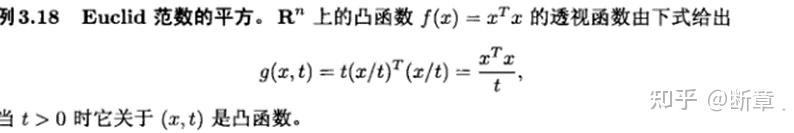




我们在微信上24小时期待你的声音
解答本文疑问/技术咨询/运营咨询/技术建议/互联网交流